Condicional

Condicional

Condicional o Implicación

Condicional de las proposiciones p y q es la proposición p ⇒ q (si p entonces q), cuya tabla de valores de verdad es de:

Variaciones de la condicional o implicación

Existen otras proposiciones relacionadas con la implicación p ⇒ q . Cualquier proposición condicional se halla conformada por un antecedente y un consecuente. Si se intercambian, se niega o las dos cosas, se forma una nueva proposición condicional.

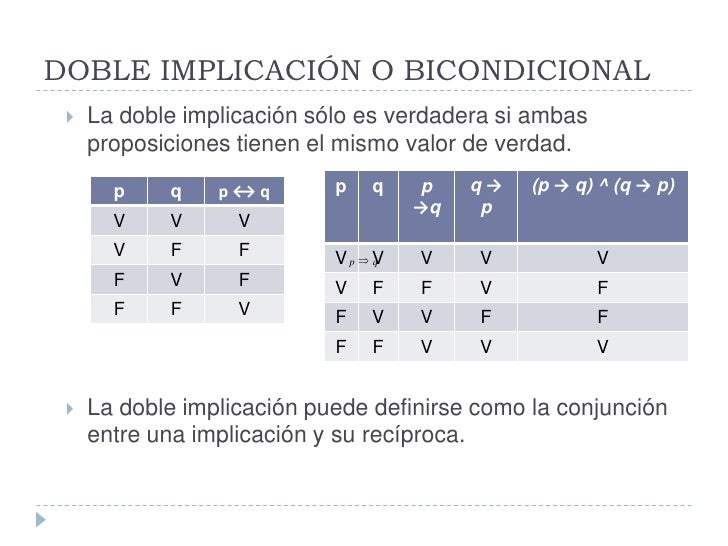
Bicondicional o Doble Implicación

Bicondicional de las proposiciones p y q en la proposición  p ⇔ q (se lee p si y solo si q), cuya tabla de valores es de:

Leyes De Morgan

Las leyes de Morgan son una parte de la lógica proposicional y analítica, creada por Augustus De Morgan  (Madura. 1806) (Londres, 1871).

las leyes De Morgan son muy útiles cuando se quieren encontrar equivalentes para proposiciones que se obtienen por negación de proposiciones compuestas. 

Negación de Condicional y la Bicondicional 

En las proposiciones ( p ⇒ q ) y  (p ⇔ q ) las equivalentes a sus respectivas negaciones son: 

Ejemplo Condicional 

p:  “llueve”

q: “hay nubes”

p→q: “si llueve entonces hay nubes”

Ejemplo Bicondiconal 

p:  “10 es un número impar”

q: “6 es un número primo”

p↔q: “10 es un número impar si y solo si 6 es un número primo”

Operaciones Proposicionales

Dadas dos o más proposiciones simples, de las cuales se conocen su valor de verdad, realizar operaciones proposicionales es determinar el valor de vedad de la proposición compuesta.

Enlace de vídeo, explicación:

https://www.youtube.com/watch?v=tKA0N8AqqiA

Comentario.

La condicional es un tema muy extenso y un poco complicado de entender a la primera, pero al darnos cuenta de su raíz y como surgen y se modifican cada una de sus variantes suele ser de gran ayuda porque es el mismo teorema que se pone en practica de acuerdo a la tabla de valores de verdad según p o q, dentro de la condicional.