Operaciones con Conjuntos.

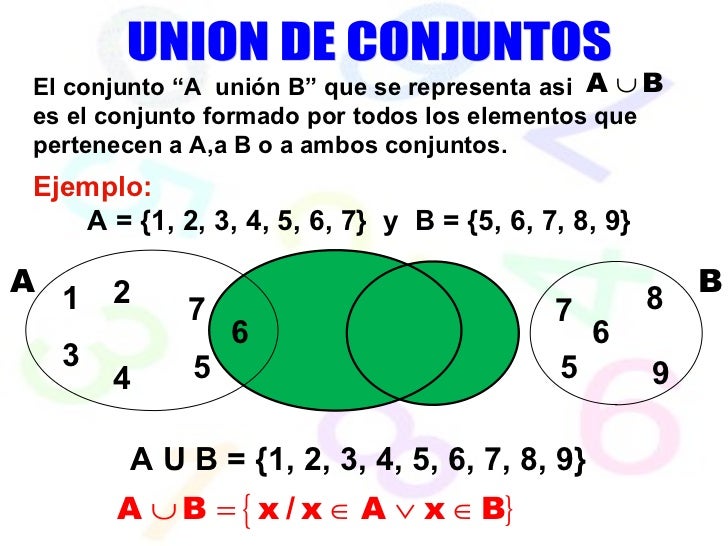
Operaciones con Conjuntos.

Operación Unión:

Consiste en reunir en un solo conjunto todos los elementos de dos o más conjuntos, el símbolo de la operación unión es: U.

Si tenemos dos conjuntos A y B, llamamos unión de A con B a un nuevos conjunto formado con os elementos que pertenecen a A o que pertenecen a B o pertenecen a ambos. }

Ejemplo:

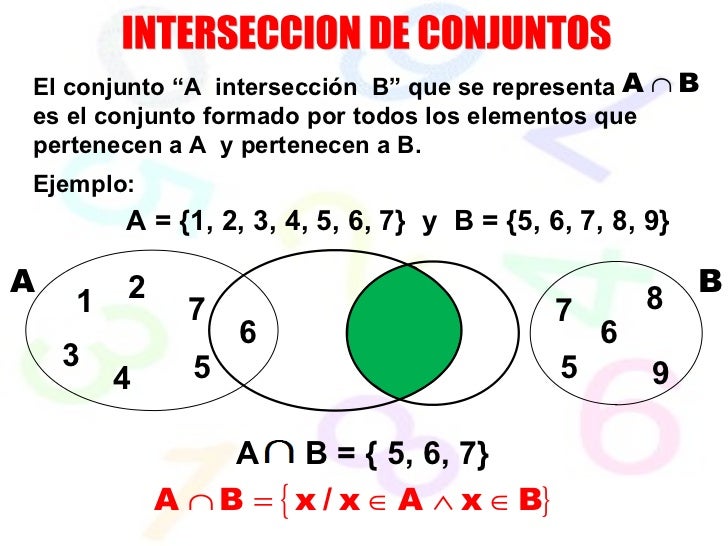
Operación Intersección:

Es formar un nuevo conjunto con los elementos comunes de los conjuntos dados, el símbolo de la operación intersección es: ⋂.

Sean los conjuntos A y B, llamamos conjunto intersección de A con B a un nuevo conjunto formado por los elementos que pertenecen a A y B a la vez.

Ejemplo:

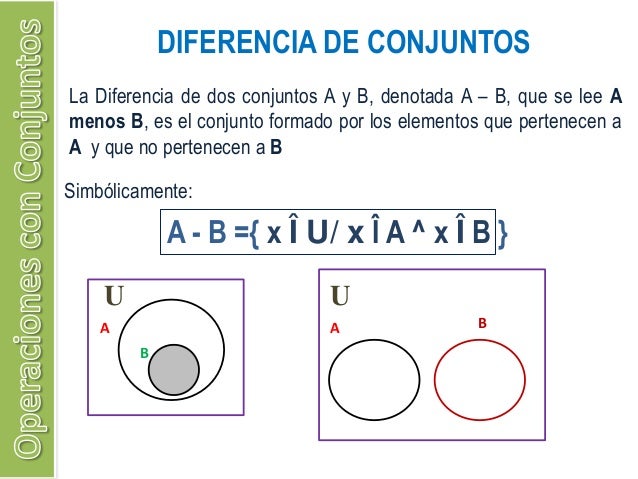
Operación Diferencia:

Dados dos conjuntos, esta operación consiste en formar un nuevo conjunto con los elementos diferentes del primero de ellos.

El símbolo de esta operación es: -

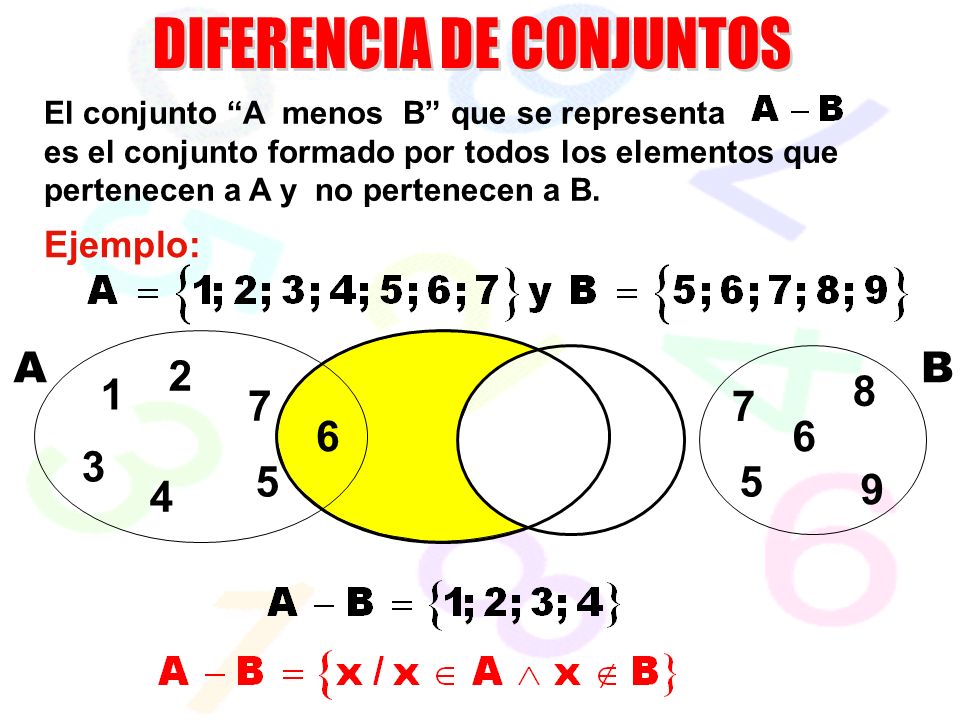
Dados los conjuntos A y B se llama diferencia de A a un nuevo conjunto formado con os elementos que pertenecen a A y que no pertenecen a B.

Ejemplo:

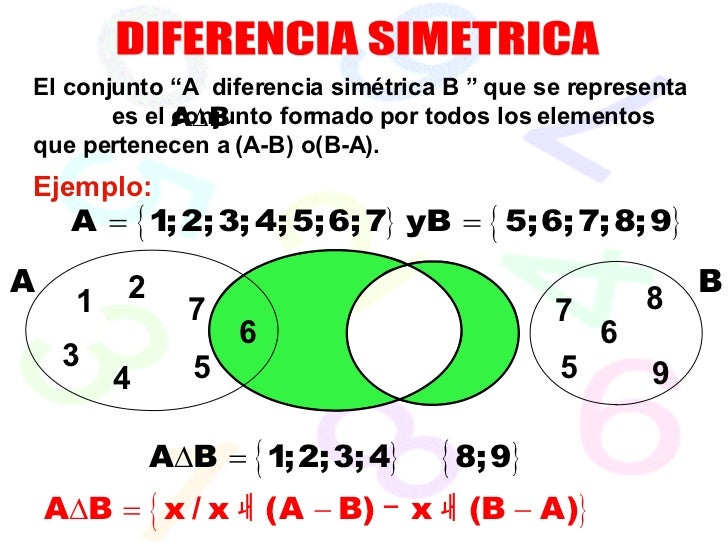
Operación  Diferencia Simétrica:

Consiste en formar un nuevo conjunto con los elementos diferentes de los dos conjuntos dados. Dados los conjuntos A y B, la diferencia simétrica de A con B es un nuevo conjunto formado con los elementos que pertenecen a A y que no pertenecen a B o elementos que pertenecen a B y que no pertenecen a A.

El símbolo de esta operación es: Δ.

Ejemplo:

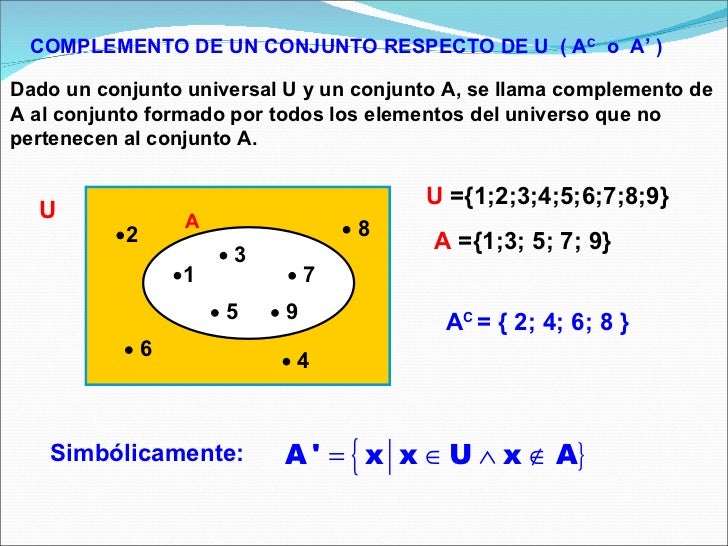
Complemento de un Conjunto:

Sea U el conjunto Referencial o Universal y A un conjunto particular contenido en este referencial, llamamos complemento de A al conjunto formado por elementos que le falta al conjunto A para ser igual al conjunto universo U.

El símbolo de la operación es: ∘

Ejemplo:

Cardinal de un Conjunto:

El cardinal de un conjunto es el número de elementos que posee. El cardinal de un conjunto A se denota por n(A) y se lee <<Número de elementos del conjunto>>.

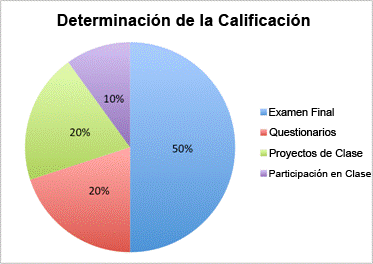
El cardinal de la unión de dos conjuntos se define como la suma de los cardinales de los conjuntos, menos el cardinal de la intersección.

Ejemplo:

Comentario.

Los conjuntos y sus operaciones nos muestra la facilidad que consiste pode unir o interceptar dos o mas conjuntos a la vez formando en si una diferencia de conjuntos simétricamente o ya sea una diferencia simple para mostrar que elementos pertenecen a cada uno de los conjuntos.

Los Conjuntos.

Los Conjuntos

Es una colección de objetos bien definidos por medio de laguna o algunas propiedades común. Por objeto entenderemos, no solo cosas físicas, como discos, computadoras, etc., sino también  abstractos, como números, letras, etc.

Conjunto Universo o Referencial

Es un conjunto formado por todos los objetos de estudio en un contexto dado.La elección de un conjunto universal se hace por conveniencia, para establecer una distinción clara entre los objetos matemáticos, todos ellos en el conjunto universal; y los conjuntos formados por dichos objetos, todos ellos subconjuntos del conjunto universal. Escogido un conjunto universal, para cada conjunto de objetos existe su complementario, que contiene todos los elementos que no están en dicho conjunto.

 Ejemplo

en aritmética los objetos de estudio son los números naturales, por lo que el conjunto universal para este caso puede ser el conjunto de los números naturales N. Al conjunto universal también se le denomina conjunto referencial, universo del discurso o clase universal, según el contexto, y se denota habitualmente por U o V.

Conjunto Intersección

Es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. 

Ejemplo

Si A = { a, b, c, d, e, f} y B = { a, e, i, o, u}, entonces la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es: A∩B = { a, e}.

Diferencia de Conjunto

Dados  dos conjuntos esta operación consiste en formar un nuevo conjunto con los elementos diferentes del primero de ellos. El símbolo de es operación es -.

Ejemplo:

Diferencia Simétrica 

Consiste en formar un nuevo conjunto con los elementos diferentes de los dos conjuntos dados. Dados los conjuntos A y B, la diferencia simétrica , de A con B es un nuevo conjunto formado con los elementos que le pertenecen a A y que no pertenecen a B o  elementos que le pertenecen a B y que no pertenecen a A.

Ejemplo

Conjunto Complementario

Sea el conjunto referencial o Universal y A un conjunto particular contenido en este referencial, llamamos complemento de A al conjunto formado por  elementos que le faltan al conjunto A para ser igual al conjunto universo U.

Ejemplo

Comentario.

Los conjuntos siendo una colección de elementos con características similares, es un tema y una forma sencilla de poder dar a conocer ciertos elementos para poder unirlos y realizar un intersección entre ellos, en su totalidad los elementos que poseen una propiedad en común que los distingue de otros también puede llamarse conjunto, ya que este esta formado por una cantidad finita o infinita de elementos.

Condicional

Condicional

Condicional o Implicación

Condicional de las proposiciones p y q es la proposición p ⇒ q (si p entonces q), cuya tabla de valores de verdad es de:

Variaciones de la condicional o implicación

Existen otras proposiciones relacionadas con la implicación p ⇒ q . Cualquier proposición condicional se halla conformada por un antecedente y un consecuente. Si se intercambian, se niega o las dos cosas, se forma una nueva proposición condicional.

Bicondicional o Doble Implicación

Bicondicional de las proposiciones p y q en la proposición  p ⇔ q (se lee p si y solo si q), cuya tabla de valores es de:

Leyes De Morgan

Las leyes de Morgan son una parte de la lógica proposicional y analítica, creada por Augustus De Morgan  (Madura. 1806) (Londres, 1871).

las leyes De Morgan son muy útiles cuando se quieren encontrar equivalentes para proposiciones que se obtienen por negación de proposiciones compuestas. 

Negación de Condicional y la Bicondicional 

En las proposiciones ( p ⇒ q ) y  (p ⇔ q ) las equivalentes a sus respectivas negaciones son: 

Ejemplo Condicional 

p:  “llueve”

q: “hay nubes”

p→q: “si llueve entonces hay nubes”

Ejemplo Bicondiconal 

p:  “10 es un número impar”

q: “6 es un número primo”

p↔q: “10 es un número impar si y solo si 6 es un número primo”

Operaciones Proposicionales

Dadas dos o más proposiciones simples, de las cuales se conocen su valor de verdad, realizar operaciones proposicionales es determinar el valor de vedad de la proposición compuesta.

Enlace de vídeo, explicación:

https://www.youtube.com/watch?v=tKA0N8AqqiA

Comentario.

La condicional es un tema muy extenso y un poco complicado de entender a la primera, pero al darnos cuenta de su raíz y como surgen y se modifican cada una de sus variantes suele ser de gran ayuda porque es el mismo teorema que se pone en practica de acuerdo a la tabla de valores de verdad según p o q, dentro de la condicional.

Proposiciones y Valores de Verdad

Proposiciones y Valores de Verdad

Proposiciones:

La proposición es el significado de una idea, enunciado conjunto de palabras o letras a las que se les puede asignar uno y solo uno de los valores de verdad, que pueden ser: verdadero (V) o falso (F), pero no ambos valores a la vez.

Por lo general, a las proposiciones se les representa por las letras del alfabeto desde la p, es decif p, q, r, s, t, etc.

Ejemplo:

p: La Universidad Rafael Landívar está en la zona 16.          Valor de verdad ( V )

r: Quetzaltenango es un departamento de Guatemala.           Valor de verdad  ( V )

s: Un quetzal es equivalente a 50 centavos.                           Valor de verdad ( F )

Proposiciones Compuestas:

Cuando un proposición consta de dos o más enunciados simples se le llama proposición compuesta o molecular. Una proposición esta compuesta cuando se construye uniendo dos o más proposiciones simples, y por ello, nos da más de una información.

Ejemplo:

Zacapa es departamento de Guatemala y pertenece a Centroamérica.

                             p                                                    q

Encontramos dos enunciados. El primero (p) nos afirma que Zacapa es departamento de Guatemala y el segundo (q) que Zacapa pertenece a Centroamérica.

Conectivos Lógicos:

A partir de proporciones simples es posible generar otras, simples o compuestas. Es decir que se puede operar con proposiciones, y para ello se utilizan ciertos símbolos llamados conectivos lógicos.

A continuación vemos una concreta definición de cada uno:

Negación: 

Dada una proposición p, se denomina la negación de p a otra proposición denotada por 〜p ( se lee <<no p>>) que se le asigna el valor de verdad al de p.

Ejemplo:

p: El kilómetro tiene 100 metros.                                                   

〜p: El kilómetro no tiene 100 metros.

Su tabla de verdad es: 

Conjunción: 
Dadas dos proposiciones p y q, se denomina conjunción de estas proposiciones a la proposición de p ∧ q ( se lee << p y q >>).

Su tabla de verdad es:

Disyunción:

Dadas dos proposiciones p y q, la disyunción de las proposiciones p y q cuya tabla de valor de verdad es:

Bicondicional o doble Implicación:

Bicondicional de las proposiciones p y q es la proposición p ⇔ q ( se lee << p  si y solo si q>>), cuya tabla de valores de verdad es:

Leyes de De Morgan:

Las leyes de De Morgan son una parte de la lógica proposicional y analítica, creada por Augustus De Morgan (Madura, 1806) (Londres, 1871).

Las leyes de De Morgan son muy útiles cuando se quieren encontrar equivalentes para proposiciones que se obtienen por negación de proposiciones compuestas.

Video de retroalimentación y ayuda.

https://www.youtube.com/watch?v=DZc9SfZdWgg

Comentario.

Cada una de estas leyes y valores son muy utilizados para hacer una proposición, ya sea su variable que diferente pero esta siempre muestra el valor que le corresponde a cada proposición según sea el criterio que se vaya a necesitar.

Lectura e Interpretación de Gráficas. Exposición, No. 1.

Gráficas.

Las gráficas son representaciones abstractas de relaciones entre dos o más variables, también resumen y organiza la información, ademas de resaltar visualmente sus propiedades más importantes, las representaciones gráficas permiten establecer patrones y transmitir ideas de modo más sencillo.

Gráficas Circulares.

Denominadas también gráficas de pastel o gráficas de 100%, se utilizan para mostrar porcentajes y proporciones, estas gráficas nos permiten ver la distribución interna de los datos que representan un hecho, en forma de porcentajes sobre un total.

Gráficas de Barras.

Se emplean para ilustrar muestras agrupadas en intervalos. Esta formada por rectángulos unidos a otros, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables, la alltura de cada rectángulo es proporcional a la frecuencia del intervalo respectivo.

Gráficas de Líneas.

Muestran la relación entre dos variables cuantitativas. En este tipo de gráfico se representan los valores en dos ejes cartesianos. Las gráficas lineales se recomienda para representar series en el tiempo y es donde se muestran valores máximos y mínimos, también se utiliza para varias muestras en un diagrama.

Pictogramas.

Es un diagrama que utiliza imágenes o símbolos para mostrar datos para una rápida visualización y comprensión. En un pictograma se utiliza una imagen o un símbolo para representar una cantidad especifica.

Gráficas Radiales.

Las gráficas radiales comparan los valores agregados de varias series de datos y muestran cambios de valores con relación a un punto central.

Enlace Interpretación de Gráficas.

https://www.youtube.com/watch?v=lzVLS3vRdNA

Comentario.

Cada uno de estos tipos de gráficas nos son muy útiles pero cada uno en su debido momento, para poder representar un dato de una manera más exacta y completa que a su vez sea fácil de poder interpretar y analizar la información que se quiera dar a conocer o mostrar. También nos puede dar una información mas detallada de una cantidad de datos o información que sea muy extensa.

Tangram sábado 29/09/2018

TANGRAM

Estos son una figuras que logramos hacer en clase.

Comentario.

El juego tangram es un gran juego de muchos acertijos al verlo parece tan simple pero oculta muchas formas y diseños que se pueden crear gracias a sus únicas 7 figuras geométricas, este rompecabezas es una forma de poder poner nuestra mente a prueba con estos ejercicios que el tangram nos trae.

Ecuaciones.

Ecuaciones

Una ecuación es un enunciado que establece que dos expresiones son iguales, en ella se incluyen términos conocidos, variables o incógnitas y signos de operación y agrupación.

Ejemplo:

Cuatro veces un número aumentado en siete unidades es igual a diecinueve. 

Sea x = el número.

Entonces                          4x + 7 = 19

La expresión 4x + 7 = 19 corresponde a n enunciado de ecuación, esta ecuación no es verdadera para todos los valores de la variable x. Los valores de x que hacen que la ecuación sea verdadera se llaman soluciones o raíces de la misma, y el proceso de determinar éstas se conoce como resolución de la ecuación.

Transposición de Términos.

El exponente nos dice el dice el grado de una ecuación.

Ejemplo:

Carolina tiene 6 años menos que su hermano José Luis. Si ambas edades suman 26 años, ¿ cuál es la edad de cada uno?

1. Comprender el problema:

¿Qué debo encontrar? La edad de Carolina y la edad de José Luis.

2. Formular un plan:

Es un problema que se puede resolver aplicando la estrategia de una ecuación de primer grado, ya que la información nos dice: edad de Carolina + edad de José Luis = 26 años. Si llamamos x a la edad de Carolina, entonces como ella es menor en 6 años que su hermano la edad de este es x + 6 y tenemos la ecuación o igualdad.

                                                               x + (x + 6) = 26

3. Llevar a cabo el plan:

Ejecutamos el plan resolviendo la ecuación de primer grado:

                                            x + (x + 6) = 26 Primero eliminamos paréntesis 

                                               x + x + 6 = 26 Luego sumamos términos semejantes

                                              2x + 6 - 6 = 26 - 6 Restamos 6 a ambos lados

      2x = 20 Dividimos ambos lados entre dos.

                                                

                                             2x                           20

                                        -----------        =       ----------

                               2                            2

         X = 10.                 10 + 6 = 16.

Entonces la edad de Carolina es 10 años y la de José Luis se ontiene sumándole 6 a la edad de Carolina y es 16.

4. Revisar y comprobar:

Esta comprobación se puede realizar sustituyendo la solución en la ecuación original y verificando la igualdad.

                                               10 + ( 10 + 6 ) = 26

                                                          10 + 16 = 26

                                                                  26 = 26

Comentario.

Las ecuaciones pueden variar según sea su grado de dificultad, siendo esta la igualdad en la que se encuentra una o varias cantidades que no conocemos y les llamamos incógnitas, estas incógnitas están representadas por letras del alfabeto, más comunes las letras X, Y, Z, 

Proporcionalidad o Porcentajes

Proporcionalidad o porcentajes

para el uso de esta estrategia necesitamos conocer ciertos conceptos fundamentales.

Razón:

Es el resultado de comparar dos cantidades y será siempre un número real.

                        

Ejemplo:

                3

   3:5 = ----- = 0.6 el resultado es un número real.

               5

Proporción:

Se le denomina proporción a la igualdad de dos razones.

Ejemplo:


       2              4
    ------   =   ------     Y leemos 2 es a 5 como 4 es a 10.
       5             10

Porcentaje:
Un porcentaje es una razón en la cual el consecuente es 100.

Ejemplo:

        8             
    --------   =   0.08 = 8%
      100             


Ejemplo:

5 cajas de chocolates cuestan Q210.00 

• ¿Cuánto costarán 8 cajas de chocolates?
• ¿Cuánto costarán 3 cajas de chocolates?

1.  Comprender el problema.

¿Qué debo encontrar? Se debe determinar cuánto costarán 8 cajas de chocolates y 3 cajas de chocolates.

2.  Formular un plan.

Si aumenta el número de cajas de chocolates también aumenta la cantidad a pagar. Lo contrario, si disminuye el número de cajas de chocolates también disminuye la cantidad a pagar. Entonces formaremos para cada pregunta una proporción (igualdad de dos razones) que relacione directamente cajas de chocolate y dinero con dinero.

3.  Llevar a cabo el plan.
Procedemos a ejecutar el plan, formando las proporciones y determinando el valor buscado.


a) Sea x el precio de 8 cajas de chocolate.

          5               8                      8 x 210
    ---------   =   ------    =        ----------------   =       Q 336.00

       210              x                          5

R/. Las 8 cajas de chocolate cuestan Q336.00.


b) Sea x el precio de 3 cajas de chocolate.
          5               3                      3 x 210
    ---------   =   ------    =        ----------------   =       Q 126.00


       210              x                          5

R/. Las 3 cajas de chocolate cuestan Q126.00.

4.  Revisar y comprobar.
Esta comprobación se puede realizar sustituyendo la solución en la proporción original y verificando la igualdad.

a)
          5                 8                  
    ---------   =   ---------    =   0.0238    



       210              336


b)
          5                 3                 
    ---------   =   ---------    =   0.0238    




       210              126

Estrategias de Razonamiento de Problemas.

Trabajar Hacia Atrás

Esta estrategia consiste en que, a partir del dato final o la solución, ir pensando hacia atrás, paso a paso hasta llegar a los datos originales. Se procede a recorrer la secuencia de pasos al contrario para ir de los datos conocidos a la solución.

Ejemplo: 

Juan al salir de su casa adquiere un libro por Q50, y después gastó en gasolina la mitad del dinero que le había quedado; luego compró alimentos por Q200 y gastó en compras de su casa la mitad del dinero que le quedó. Regresa a casa con Q100. ¿Con cuánto dinero salió Juan de su casa?

1. Comprender el Problema:

¿Qué debo encontrar?  ¿Con cuánto dinero salió Juan de su casa?

2. Formular un Plan:

La estrategia para resolver este problema es trabajar hacia atrás.

3. Llevar a Cabo el Plan.

Gasto de compras= Q 100 x 2 = Q 200.

Alimentos por Q 200 = Q 200 + Q200 = Q 400.

Gasolina= Q 400 x 2 = Q 800.

Precio del Libro Q 50 + Q 800 = Q 850.

4. Revisar y Comprobar:

Precio del Libro = Q 850. - Q 50. = Q 8500.

Gasolina = Q 800. / 2 =  400

Alimentos por Q 200 = Q 400 - Q 200 = Q 200.

Gasto en compras de casa = Q200 / 2 = Q 100.

De esta manera se comprueba que que la respuesta es correcta.

Hacer Un Diagrama o Figura

En la mayoría de problemas es útil dibujar un diagrama o esquema, e identificar en ellos daros e incógnitas del problema. En la figura se colocan todos los datos conocidos que da el problema y los datos que se pretende encontrar, esto nos ayuda a tener una mejor idea y visualización de lo que el problema pide.

Ejemplo:

Resolver un Problema Equivalente

Varios problemas se pueden resolver al visualizar un problema equivalente. Esta estrategia consiste en comparar el problema con otro parecido, cuya solución se conoce o es más fácil de resolver y relacionarlo con el nuevo problema.

Ejemplo:

Comentario Personal.

Cada uno de estos pasos nos demuestra su facilidad para poder resolver cada problema de una manera mas sencilla. 

La estrategia trabajar atrás nos da la facilidad de encontrar lo que nos piden de una manera que debemos operar todo el problema de manera invertida. 

La estrategia hacer un diagrama o una figura nos da la facilidad de poder hacer una lista o un dibujo de como plantearemos el problema para darle una solución de manera mas sencilla.

La estrategia de resolver un problema equivalente nos da la ventaja de poder comparar el problema con otro tratando de encontrar y diferenciar el patrón el cual debemos seguir.